3 Datos: tipos y estructuras

En términos genéricos, todos los elementos que maneja R son objetos: un valor numérico es un objeto, un vector es un objeto, una función es un objeto, una base de datos es un objeto, un gráfico es un objeto…

Para realizar un uso eficiente de R es preciso entender y aprender a manipular bien las distintas clases de objetos que maneja el programa. En esta sección nos vamos a ocupar particulamente de aquellos objetos que R utiliza para representar datos: valores, vectores, matrices, dataframes y listas.

3.1 Tipos de datos

La unidad básica de datos en R es un vector, los cuales pueden ser de diferentes clases. Los que más usaremos son las siguientes cuatro clases.

Clase Ejemplo
numeric c(12.3, 5, 999)
logical c(TRUE, FALSE)
integer c(2L, 34L, 0L)
character c(‘a’, ‘good’, ‘TRUE’, ‘23.4’)

3.1.1 Vectores

# concatenación de elementos atómicos
v <- c(8, 7, 9, 10, 10, 111)
class(v)

(b <- c("A", "b"))
class(b)

(b1 <- c("12", "30"))
is.numeric(b1)
is.character(b1)

(m <- c(TRUE, FALSE, T, F)) ; class(m)

# Propiedades de v
# ?length
length(v)  
summary(v) 
sort(v)
  • Operaciones con vectores
v - 1

# Medidas de posición
mean(v) 
median(v)

# Medidas de dispersión
var(v)
sd(v)
sqrt(var(v))
IQR(v)
range(v)
max(v)
min(v)
sum(v)

#v1 <- edit(v) #typo
v1
hist(v1)
plot(density(v1))
p10 = quantile(v1, 0.1)
abline(v = p10, col = "red")

summary(v)

Regenerar summary() a traves de funciones individuales

Cree tres nuevos vectores que sean: a) la potencia cuadrada de 3.5 de v; b) la raíz cúbica de v; c) el logaritmo natural de la diferencia de a) y b)

  • Secuencia
1:7  
seq(from = 0, to = 20, #by=2) # 
    length=4) 

rep(1:3, times=3) #  , each=3

3.1.2 Números aleatorios

La generación de números aleatorios es en muchas ocasiones un requerimiento esencial en investigación científica. Proceder de este modo puede reducir cualquier sesgo generado por nuestra persona a la hora de seleccionar una muestra, o aplicar un tratamiento a una unidad experimental.

  • Generar números enteros de modo aleatorio de una muestra determinada

sample()

sample(1:30, size=10, replace=F) #sin reposición
  • Generar números aleatorios de una distribución específica de parámetros conocidos:

runif() - números racionales aleatoriamente, uniformemente distribuidos en un intervalo

num_unif <- runif(100, min=3, max=4)
hist(num_unif)

rnorm() - números aleatorios, pertenecientes a una población con distribución normal, con parámetros μ y σ.

num_norm <- rnorm(100, mean=70, sd=5) 
hist(num_norm)

Vamos a recrear estas muestras partiendo de la información contenida en la tabla

(Parra-Bracamonte et al. 2007) 
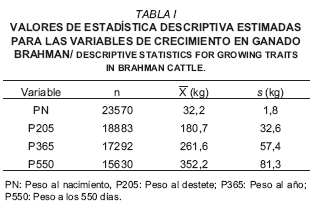
set.seed(123)
PesoNac <- rnorm(23570, mean=32.2, sd=1.8) 
range(PesoNac)
hist(PesoNac)
hist(PesoNac, prob=TRUE)
  • Propiedades de vectores

Si colocáramos dos o más clases diferentes dentro de un mismo vector, R va forzar a que todos los elementos pasen a pertenecer a una misma clase. El número 1.7 cambiaría a “1.7” si fuera creado junto con “a”.

y1 <- c(1.7, "a")  ## character
class(y1)

y2 <- c(TRUE, 0, 10)   ## numeric
class(y2)

y3 <- c(TRUE, "a") ## character
class(y3)

y4 <- c(T, F)
class(y4)

as.numeric(y1)
as.numeric(y3)
as.numeric(y4)

as.logical(y2)

# character > numerico > logico

Forzando las clases explícitamente

as.character(), as.numeric(), as.integer() y as.logical()

  • Factores

Conceptualmente, en R, los factores son variables categóricas con un número finito de valores o niveles (levels). Son variables clasificadoras o agrupadoras de nuestros datos. Uno de los usos más importantes de los factores es en el modelado estadístico, dado que éstos son considerados de manera diferente a las variables contínuas. Claro ejemplo de factores son los tratamientos, por ej: fungicidas, genotipos, bloques, etc.

Los niveles de un factor pueden estar codificados como valores numéricos o como caracteres (labels). Independientemente de que el factor sea numérico o caracter, sus valores son siempre almacenados internamente por R como números enteros, con lo que se consigue economizar memoria.

Podemos comprobar que la ordenación de los niveles es simplemente alfabética.

clones = c("control", "B35", "A12", "T99", "control", "A12", "B35", "T99", 
"control", "A12", "B35", "T99", "control")
class(clones)
levels(clones)

clones_f = factor(clones)
levels(clones_f)
table(clones_f)

Las variables numéricas y de caracteres se pueden convertir en factores (factorizar), pero los niveles de un factor siempre serán valores de caracteres. Podremos verlo en el siguiente ejemplo:

vec <- c(3, 5, 7, 1)
sum(vec);mean(vec)

vec_f <- factor(vec)
vec_f
levels(vec_f)
sum(vec_f);mean(vec_f)

vec_n  <- as.numeric(vec_f)
vec_f
vec_n
sum(vec_n); mean(vec_n)

¿Cómo hizo la transformación R? Hemos recuperado los valores numéricos originales (vec)? que representan los números codificados por R en vec_f?

vec_f1 = as.numeric(as.character(vec_f))
sum(vec_f1);mean(vec_f1)
  • Condición
# ifelse(condición, valor_si_TRUE, valor_si_FALSE)
ifelse(y<2, "Low", "High")

Se evaluaron 10 clones de porta-injertos de cítricos según su resistencia a Gomosis del Tronco (Phytophthora parasitica). Los diámetros de la lesión (cm) en el punto de inoculación fueron: 3, 6, 1, 10, 3, 15, 5, 8, 19, 11.

Crear un vector “resist” con las categorías S o R, “S” aquellos clones con lesiones por encima de la mediana, y “R” clones con lesiones por debajo de la mediana.

  • Indexación
y <- 1:10
y[ ]
y[2]
y[1:3]

Seleccione los elementos 1° y 3°


3.1.3 Valores especiales

Existen valores reservados para representar datos faltantes, infinitos, e indefiniciones matemáticas.

  • NA (Not Available) significa dato faltante/indisponible. El NA tiene una clase, o sea, pueden ser NA numeric, NA character, etc.
y <- c(2, 4, NA, 6)
is.na(y)

Calcule el promedio de y (use la ayuda de R en caso necesario)mean(y)

  • NaN (Not a Number) es el resultado de una operación matemática inválida, ej: 0/0 y log(-1). Un NaN es un NA, pero no recíprocamente.
0/0
is.nan(0/0)
is.na(0/0)
  • NULL es el vacío de R. Es como si el objeto no existiese
a = NULL
a
  • Inf (infinito). Es el resultado de operaciones matemáticas cuyo límite es infinito, es decir, es un número muy grande, por ejemplo, 1/0 o 10^310. Acepta signo negativo -Inf.
1/0
1/Inf

3.2 Estructura de datos

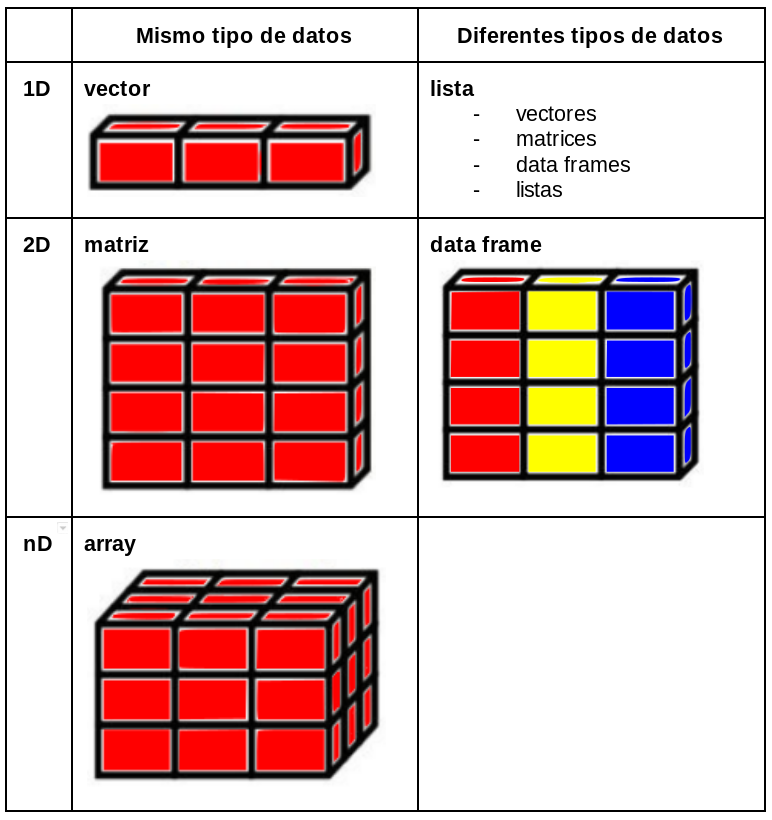
3.2.1 Data frames

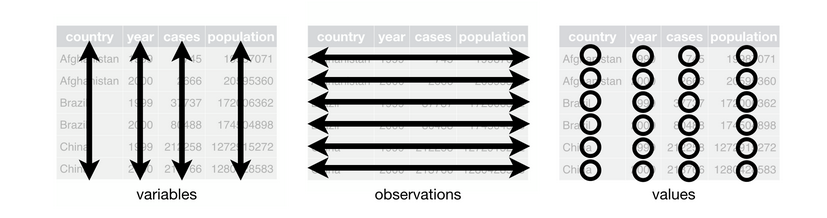
Conjunto de observaciones (filas) y variables (columnas). A diferencia que en las matrices, las columnas pueden tener diferentes tipos (clases) de variables como por ejemplo numéricas, categóricas, lógicas, fechas.

Un dataframe es completo con dimensiones n_fila x p_columna, donde:

1- Cada fila debe contener toda la info de la unidad experimental que se está evaluando

2- Cada columna representa una variable (descriptiva o respuesta)

3- Cada celda debe tener su observación (en caso de faltar el dato será un NA)

En numerosos paquetes de R, hay data frames disponibles para ejemplos de aplicación de funciones. Un ejemplo muy usado, que está en el paquete base es el dataset “iris”.

?iris
View(iris) # ya activo desde inicio de sesión por default

hacer lo mismo con los respectivos shortcuts

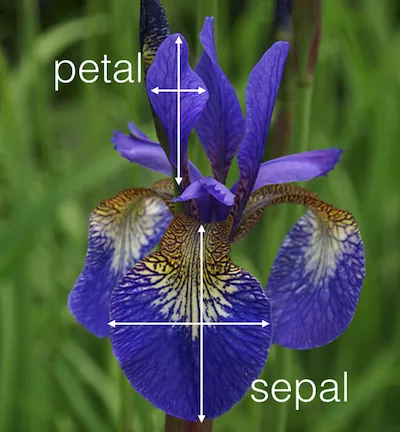
Explore el dataset iris con las siguientes funciones con iris y anote sus resultados:
dim(); head(); tail();names(); str(); summary()

  • Filtrado de datasets

data[fila, columna]

iris[1,]
iris[,1]
iris[1,1]

iris$Sepal.Length
levels(iris$Species)

identical(iris$Petal.Width, iris[,2])

Selecione: i) la segunda fila; ii) la segunda columna; iii) la observación ubicada en la 2° fila y 3° columna; iv) las observaciones de las líneas 50 a 60 de las columnas 3 y 4; v) las observaciones de las líneas 50 a 60 de las columnas 2 y 4.

3.2.2 Listas

Objetos que aceptan elementos de clases diferentes.

x <- list(a = 1:5, b = c("a", "b"), c = TRUE)
x

(Más info de subsetting elementos de una lista aquí)

x$a       # 
x[1]       # 
#sum(x[1])
x[[1]]     # 
sum(x[[1]])
x["c"]     #

3.2.3 Matrices

Indicamos el número de filas con el argumento nrow y con ncol el número de columnas; luego indicamos qué valores forman la matriz (del 1 al 9), y le hemos pedido a R que use esos valores para rellenar la matriz A por filas con byrow=TRUE. La matriz A así construida es:

A <- matrix(nrow=3, ncol=3, c(1,2,3,4,5,6,7,8,9), byrow=TRUE)

Al igual que para los dataframes, se pueden seleccionar partes de una matriz utilizando los índices de posición [fila, columna] entre corchetes.

A[2,3]   # Se selecciona el valor de la fila 2, columna 3

Referencias

Parra-Bracamonte, Gaspar Manuel, Juan Carlos Martı́nez-González, Francisco Javier Garcı́a-Esquivel, Arnoldo González-Reyna, Florencio Briones-Encinia, and Eugenia Guadalupe Cienfuegos-Rivas. 2007. “Tendencias Genéticas Y Fenotı́picas de Caracterı́sticas de Crecimiento En El Ganado Brahman de Registro de México.” Revista Cientı́fica 17 (3): 262–67.